(1)在数论,特别是整除理论中,原根是一个很重要的概念。
对于两个正整数 ,由欧拉定理可知,存在正整数
,由欧拉定理可知,存在正整数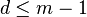 , 比如说欧拉函数
, 比如说欧拉函数 ,即小于等于 m 的正整数中与 m 互质的正整数的个数,使得
,即小于等于 m 的正整数中与 m 互质的正整数的个数,使得 。由此,在
。由此,在 时,定义
时,定义 对模
对模 的指数
的指数 为使
为使 成立的最小的正整数
成立的最小的正整数 。由前知
。由前知 一定小于等于
一定小于等于  ,若
,若 ,则称
,则称 是模
是模 的原根。
设
的原根。
设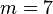 ,则
,则 等于6。
等于6。
- 设
 ,由于
,由于 ,而
,而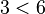 ,所以 2 不是模 7 的一个原根。
,所以 2 不是模 7 的一个原根。 - 设
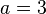 ,由于
,由于 ,
, ,
,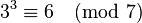 ,
, ,
, ,
, ,因此有
,因此有 ,所以 3 是模 7 的一个原根。
,所以 3 是模 7 的一个原根。
(2)原根的一些性质
- 可以证明,如果正整数
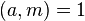 和正整数 d 满足
和正整数 d 满足 ,则 d 整除
,则 d 整除  。因此
。因此 整除
整除 。在例子中,当
。在例子中,当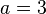 时,我们仅需要验证 3 的 1 、2、3 和 6 次方模 7 的余数即可。
时,我们仅需要验证 3 的 1 、2、3 和 6 次方模 7 的余数即可。
- 记
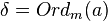 ,则
,则 模 m 两两不同余。因此当
模 m 两两不同余。因此当 是模
是模 的原根时,
的原根时, 构成模 m 的简化剩余系。
构成模 m 的简化剩余系。
- 模
 有原根的充要条件是
有原根的充要条件是 ,其中
,其中 是奇质数,
是奇质数, 是任意正整数。
是任意正整数。