快速幂顾名思义,就是快速算某个数的多少次幂。其时间复杂度为 O(log₂N), 与朴素的O(N)相比效率有了极大的提高。
以下以求a的b次方来介绍
把b转换成二进制。
该二进制数第i位的权为
 例如
例如
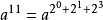
11的二进制是1011 11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1 因此,我们将a¹¹转化为算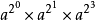 ------百度百科
例子:计算A23,23用二进制展开(10111):
23 = 1 * 24 +
0 * 23 + 1 * 22 +
1 * 21 + 1 * 20,
迭代从低位开始,第k位为0,即不操作;第k位为1,base *2k-1。
------百度百科
例子:计算A23,23用二进制展开(10111):
23 = 1 * 24 +
0 * 23 + 1 * 22 +
1 * 21 + 1 * 20,
迭代从低位开始,第k位为0,即不操作;第k位为1,base *2k-1。
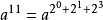
11的二进制是1011 11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1 因此,我们将a¹¹转化为算
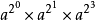 ------百度百科
例子:计算A23,23用二进制展开(10111):
23 = 1 * 24 +
0 * 23 + 1 * 22 +
1 * 21 + 1 * 20,
迭代从低位开始,第k位为0,即不操作;第k位为1,base *2k-1。
------百度百科
例子:计算A23,23用二进制展开(10111):
23 = 1 * 24 +
0 * 23 + 1 * 22 +
1 * 21 + 1 * 20,
迭代从低位开始,第k位为0,即不操作;第k位为1,base *2k-1。
int fun(int a,int b)
{
int r=1,base=a;
while(b!=0)
{
if(b&1) //判断当前数的奇偶
r*=base;
base*=base;
b>>=1; //右移
}
return r;
}
快速幂取模算法基础在于模运算的基本性质: (a*b)%m = ( (a%m) * (b%m) ) %mint fun(int a,int b,int m)
{
int r=1,base=a;
while(b!=0)
{
if(b&1) //判断当前数的奇偶
r=r*base%m;
base=base*base%m;
b>>=1;
}
return r;
}
矩阵的快速幂是用来高效地计算矩阵的高次方的。将朴素的o(n)的时间复杂度,降到log(n)。
这里先对原理(主要运用了矩阵乘法的结合律):
一般一个矩阵的n次方,我们会通过连乘n-1次来得到它的n次幂。
但做下简单的改进就能减少连乘的次数,方法如下:
把n个矩阵进行两两分组,比如:A*A*A*A*A*A => (A*A)*(A*A)*(A*A)
这样变的好处是,你只需要计算一次A*A,然后将结果(A*A)连乘自己两次就能得到A^6,即(A*A)^3=A^6。算一下发现这次一共乘了3次,少于原来的5次。
矩阵的快速幂问题,和一般数的快速幂基本一样(二进制位按权值展开),下面举个例子进行说明:
现在要求A^156,而156(10)=10011100(2)
也就有A^156=>(A^4)*(A^8)*(A^16)*(A^128) 考虑到因子间的联系,我们从二进制10011100中的最右端开始计算到最左端。
下面以hdu 1575为例:
A为一个方阵,则Tr A表示A的迹(就是主对角线上各项的和),现要求Tr(A^k)%9973。//矩阵快速幂 任何矩阵乘以单位矩阵,其值不改变。
#include
#include
#include
const int N=10,Mod=9973;
struct Matrix
{
int m[N][N];
};
int n;
Matrix Mul(Matrix a,Matrix b) //矩阵乘法
{
Matrix c;
memset(c.m,0,sizeof(c.m));
for(int i=0;i>=1;
a = Mul(a,a);
}
return res;
}
int main()
{
int t,k,sum;
scanf("%d",&t);
Matrix a;
while (t--)
{
sum=0;
scanf("%d%d",&n,&k);
for (int i=0; i